前言

本文是结合《数据库系统概念》的摘要、上课ppt和b站战德臣老师的网课《数据库系统》所作的笔记，自用。

---

第2章：关系模型介绍

2.1 关系数据库的结构

关系数据库由表的集合构成，每个表有唯一的名字，表中描述了一批相互有关联关系的数据。
关系是元组（一组值的序列）集合，元组在关系中出现的顺序无关紧要

• 关系——表
• 元组——行
• 属性——列，属性值一定是原子的
• 关系实例——表示一个关系的特定实例，也就是所包含的一组特定的行
• 域——对于关系的每个属性，都存在一个允许取值的集合
• 原子性——域中单元的不可分割性
• 空——是一个特殊的值，表示值未知或不存在

2.2 数据库模式

数据库模式：数据库的逻辑设计
数据库实例：给定时刻数据库中数据的一个快照

2.3 码/键

码/键：区分唯一一个元组的属性值。
超码：一个或多个属性的集合，这些属性的组合可以使我们在一个关系中唯一地表示一个元组。
候选码：超码的任意子集都不能超码，这样的最小超码称为候选码。候选码不唯一。
主码：代表被数据库设计者选中的、主要用来在一个关系中区分不同元组的候选码；主码应该选择值从不或极少变化的属性。
外码：一个关系模式（r1）可能在它的属性中包括另一个关系模式（r2）的主码，这个属性在r1上被称作参照r2的外码；r1也称为外码依赖的参照关系，r2叫做外码的被参照关系。
参照完整性约束：要求在参照关系中任意元组在特定属性上的取值必然等于被参照关系中某个元组在特定属性上的取值。

2.4 模式图

一个含有主码和外码依赖的数据库模式可以用模式图来表示。
主码的属性用下划线标注。

2.5 关系查询语言

查询语言：是用户用来从数据库中请求获取信息的语言；查询语言可以分为：

• 过程化语言——用户指导系统对数据库执行一系列操作以计算出所需结果
• 非过程化语言：用户只需描述所需信息，而不用给出获取该信息的具体过程

关系代数包括一个运算的集合，这些运算以一个或两个关系为输入，产生一个新的关系作为结果。
关系演算使用谓词逻辑来定义所需的结果，但不需给出获取结果的特定代数过程。

2.6 关系运算

两个关系上的自然连接运算所匹配的元组在两个关系共有的所有属性上取值相同。
关系代数：定义了在关系上的一组运算。

---

---

第6章：形式化关系查询语言

6.1 关系代数

关系代数是一种过程化查询语言。他是一个运算的集合。

• 运算一般以一个或两个关系为输入，产生新的关系作为结果。
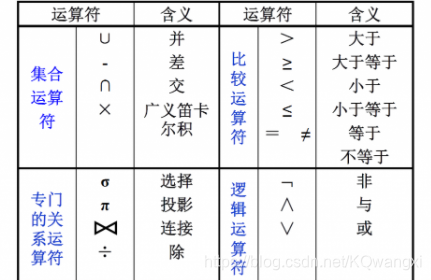
• 基本运算包括：选择、投影、并、集合差、笛卡尔积、更名、集合交、自然连接和赋值。

集合操作：并、交、差、笛卡尔积
纯关系操作：投影、选择、连接、除

6.1.1 基本运算

首先关系代数运算具有一定约束，比如并、差、交等，需满足并相容性。
并相容性：

• 参与运算的两个关系及其相关属性之间有一定的对应性、可比性或意义关联性
• 定义：关系R与关系S存在相容性，当且仅当：
  （1）关系R和关系S的属性数目必须相同；
  （2）对于任意i，关系R的第i个属性的域必须和关系s的第i个属性的域相同

一元运算：选择、投影、更名

6.1.1.1 选择

• 定义：给定一个关系R，同时给定一个选择的条件condition（简记con），选择运算结果也是一个关系，记作：σ _con （ R ），它从关系R中选择出满足给定条件condition的元组构成（也就是行）。
• 数学描述：σ _con （ R ）= { t | t ∈ R ∧ con(t) = ‘真’ }，下面几点为注意事项：
  • 设R（A1,A2,……,An）,t是R的元组，t的分量记为t[Ai]，或简写为Ai
  • 条件con由逻辑运算符连接比较表达式组成
  • 表达式中涉及到字符常量要加双引号
  • 逻辑运算符：∨ ，∧，┐，或者也可以写为 and，or，not
  • 比较表达式：X θ Y，其中X,Y是t的分量、常量或简单函数，θ是比较运算符，θ ∈{＝、≠、<、≤、>、≥}
  • 运算符的优先次序，优先次序自高至低为{ 括弧；θ；┐； ∧；∨}

举例——从instructor关系表中找出所有属性栏dept_name为Physics的所有单元
σ_{dept_name=“Pysics”}（instructor)

6.1.1.2 投影

• 定义：给定一个关系R，投影运算结果也是一个关系，记作：Π_A（R），它从关系R中选出属性包含在A中的列构成。

• 数学描述：Π_{Ai1，Ai2，……，Aik}（R）= { <t[Ai1],t[Ai2],……t[Ain]> | t ∈ R}

  • 设R（A1，A2,……A3）
  • {Ai1,Ai2,……Ajk}⊆{A1，A2，……，An}
  • t[Ai]表示元组t中相应于属性Ai的分量
  • 投影运算可以对原关系的列在投影后重新排列

• 投影操作从给定关系中选出某些列组成新的关系，而选择操作是从给定关系中选出某些行组成新的关系。

在原关系列表中进行挑选，返回作为参数的关系，而把某些属性排除在外。投影用Π表示，列举希望出现的属性作为Π的下标，用逗号分隔：
Π_{feature1，feature2}（relationTable）
2)举例——查询instructor中ID、name、salary的属性
Π_{ID，name，salary}（instructor）

6.1.1.3 并运算

• 定义：假设关系R和关系S是并相容的，则关系R与关系S的并运算结果也是一个关系，记作——R ∪ S，它由或者出现在关系R中或者出现在S中的元组构成。
• 数学描述：R ∪ S = {t | t ∈ R ∨ t ∈ S} ，其中t为元组。
• 并运算是两个关系的元组合合并成一个关系，在合并时去掉重复的元组。

举例——找出开设在2009年秋季学期或者2010年春季学期或者二者皆开的所有课程的集合：
Π_{couser_id}（ σ_{semester="Fall"∧year=2009}（section)）∪ Π_{couser_id}（ σ_{semester="Spring"∧year=2010}（section)）

并运算 r ∪ s需要满足并相容性：
1）r与s的属性数目必须相同
2）对所有的i，r的第i个属性的域必须和s的第i个属性的域相同。

6.1.1.4 差

• 定义：假设关系R和关系S是并相容的，则关系R与关系S的差运算结果也是一个关系，记作：R-S，它由出现在关系R中但不出现在关系S中的元组构成。
• 数学描述：R - S = { t | t ∈ R ∧ t ∉ S}，其中t是元组。

举例——找出所有开设在2009年秋季学期但是在2010年春季学期不开的课程：
Π_{couser_id}（ σ_{semester="Fall"∧year=2009}（section)）— Π_{couser_id}（ σ_{semester="Spring"∧year=2010}（section)）

同样的，减运算r-s也需要满足并相容性：
1）r与s的属性数目必须相同，r与s同元
2）对所有的i，r的第i个属性的域必须和s的第i个属性的域相同。

6.1.1.5 广义笛卡尔积

• 定义：关系R（<a1,a2,……,an>）与关系S（<b1,b2,……,bn>）的广义笛卡尔积运算结果也是一个关系，记作：R x S，它由关系R中的元组与关系S中的元组进行所有可能的拼接构成。
• 数学描述：R x S ={ <a1,a2,……,an,b1,b2,……,bn>|<a1,a2,……,an>∈R ∧ <b1,b2,……,bn>∈S }

举例——找出所有物理系的所有老师，以及他们教授的所有课程：
σ_{instructor.ID=tachers.ID"}((σ_{dept_name=“Pysics”}（instructor x teachers)）

6.1.1.6 更名

给关系代数表达式的结果进行命名。用小写希腊字母ρ表示更名运算：
1)ρ_x（E）
式子含义：E为关系表达式，返回表达式E的结果并把名字x赋给E
2)ρ_{x(A1,A2,A3……,An）}(E）
式子含义：E为关系表达式，返回表达式E的结果并把名字x赋给E,同时将各属性更名为A1,A2,A3……,An
举例——找出大学里最高工资：
Π_salary（instructor）— Π_{instructor.salary}（ σ_{instructor.salary<d.salary}(instructor x ρ_d（instructor)))
其中更名运算不是必需，因为可以对属性使用位置标记：
instructor.salary=$4
d.salary=$8
$表示位置定位，数字即为属性下标，故上诉表达式可改为：
Π_salary（instructor）— Π_$4（ σ_$4<$8(instructor x ρ_d（instructor)))

6.1.1.7 除运算

• 除法运算经常用于求解“求解……全部的/所有的”问题
• 前提条件：给定关系R(A1,A2,……,An)为n度关系，关系S(B1,B2,……,Bm)为m度关系，如果可以进行关系R与关系S的除运算，当且仅当：属性集{B1,B2,……,Bm}是属性集{A1,A2,……,An}的真子集，即m<n。
• 定义：关系R和关系S的除运算结果也是一个关系，记作：R ➗ S。

R ➗ S = Π_R-S（R）— Π_R-S（ ( Π_R-S( R ) x S) — R)

R ➗ S结果的属性：①设属性集{C1,C2,……,Ck}={A1,A2,……,An} — {B1,B2,……,Bm},则k=n-m；②如下图所示

6.1.2 关系代数的形式化定义（基本操作）

• E₁ ∪ E₂
• E₁ - E₂
• E₁ x E₂
• σ_p（E₁）
• Π_s(E₁)
• ρ_x(E₁)

6.1.3 附加的关系代数运算

以下扩展操作的定义来源是因为它们都可以由上述的基本操作进行组合得到。

6.1.3.1 集合交运算

• 定义：假设关系R和关系S是并相容的，则关系R与关系S的交运算结果也是一个关系，记作：R ∩ S，它由同时出现在关系R和关系S中的元组构成。
• 数学描述：R ∩ S= { t | t ∈ R ∧ t ∈ S }，其中t是元组
• 集合交的关系代数表达式都可以通过一对集合差运算替代集合交运算来重写：R ∩ S=R -（R - S）=S - ( S - R )

6.1.3.2 连接运算

①自然连接

• 定义：给定关系R和关系S，R与S的自然连接运算结果也是一个关系，记作R ⋈ S，它由关系R和关系S的笛卡尔积中选取相同属性组B上值相等的元组所构成。
• 数学描述：R ⋈ S = σ_t[A]=s[B](R x S)
  • 自然连接类似于笛卡尔积，但自然连接是一个特殊的等值连接，只有当R,S属性相同，值相等才能连接。同时自然连接会对结果中去掉重复的属性列（即去重）。
• 如果关系t（R）和s（S）不含有任何相同属性，即 R ∩ S=Φ，那么 R ⋈ S = R x S
• 自然连接是可结合的

②θ连接

• 定义：给定关系R和关系S，R与S的θ连接运算结果也是一个关系，记作：R ⋈_(AθB) S，它由关系R和关系S的笛卡尔积中，选取R中属性A与S中属性B之间满足θ条件的元组构成。
  • θ连接是自然连接的扩展，它使得我们可以把一个选择运算和一个笛卡尔积运算合并为单独的一个运算，如下所示。
• 数学描述：R ⋈ S = σ_t[A]θs[B](R x S)，t是关系R中的元组，s是关系S中的元组，θ是比较运算符，θ ∈{＝、≠、<、≤、>、≥}

6.1.3.3 赋值运算

赋值运算用 ← 表示，往往用于给临时变量赋值，例如：

temp1 ← R x S
temp2 ← σ_{r.A1=s.A1∧r.A2=s.A2∧……∧r.An=s.An}（temp1）
result=Π_R∪S（temp2）

6.1.3.4 外连接运算

外连接运算时连接运算的扩展，可以处理缺失的信息。它在结果中创建带空值的元组，以此来保留在连接中丢失的那些元组。所以外连接=自然连接（或θ连接）+失配的元组（与全空元组形成的连接）。
外连接运算的三种形式：

1. 左外连接：⟕
   左外连接=自然连接（或θ连接）+左侧表中失配的元组
   记作R ⟕ S
   取出左侧关系中所有与右侧关系的任一元组都不匹配的元组，用空值填充所有来自右侧关系的属性，再把产生的元组加到自然连接的结果中。所有来自左侧关系关系的信息在左外连接结果中都得到了保留。

2. 右外连接：⟖
   右外连接=自然连接（或θ连接）+右侧表中失配的元组
   与左外连接相对成：用空值填充所有来自右侧关系的所有与左侧关系的任一元组都不匹配的元组，将结果加到自然连接的结果中。所有来自右侧关系关系的信息在右外连接结果中都得到了保留。

3. 全连接：⟗
   全外连接=自然连接（或θ连接）+两侧表中失配的元组
   既做左外连接，又做右外连接，既填充左侧关系中与右侧关系的任一元组都不匹配的元组，又填充右侧右侧关系中与左侧关系的任一元组都不匹配的元组，并把结果都加到连接的结果中。

6.1.3.5 运算的组合训练

（以下仅作简要表示，体会关系代数中各种限制条件的判断写法，具体表格就不列出啦，别问为啥下面这么排版，因为别的好看的又能保证关系代数表达式不换行的我不会）

例子	空白栏
举例①：找出物理系所有教师的名字
Πname（σdept_name=“Pysics”（instructor)）
分隔
举例②：查询学习课程号为002的学生号和学生学期总成绩（学生号与成绩均在表格SC中）
Πstudent_id，score（σC#=“002”（SC)）
分隔
举例③:查询学习课程号为001的学生学号和姓名（学生学号在SC表中，而学生姓名在Student表中，同时Student和SC有公共属性栏：学生学号）
Πstudent_id，student_name（σC#=“001”（ Student ⋈ SC )）
③的另一种写法,我们不难发现其实就是将上面的自然连接换为了关系在某种条件下的笛卡尔乘积
Πstudent_id，student_name（σC#="001"∧Student.student_id=SC.student_id（ Student x SC )）
分隔
举例④:查询学习课程名称为数据结构的学生学号、姓名和这门课程的成绩（学生学号在SC表中，学生姓名在Student表中，课程成绩在Course表中；Student和SC有公共属性栏为：学生学号；SC与Course的公共属性栏为：课程号）
Πstudent_id，student_name,course_score（σC_name=“数据结构”（ Student ⋈ SC ⋈ Course )）
分隔
举例⑤：查询学习了课程号为001或002的学生的学号
Πstudent_id（σC#="001"∨C#=“002”（ SC )）
分隔
举例⑥：查询至少学习了课程号为001和002的两门课的学生的学号
ΠSC.student_id（σSC.C#="001"∧SC1.C#=“002”（ SC ⋈ ρSC1( SC））） ，正确写法是使用等值连接，⋈ 连接的条件为SC.C#=SC1.C#
当然上述也可以采用交运算实现
Πstudent_id（σ~SC.C#=“001”（SC））∩ Πstudent_id（σ~SC.C#=“002”（SC））
下方⑥的另一种写法是一个很经典的错误示范！因为选择操作是对关系中的每一条记录进行筛选，而每一条记录在筛选的时候要么c#=001，要么c#=002，绝对不存在某一个属性值可以同时等于多个值，所以右侧语句选出来一定是个空集。
Πstudent_id（σC#="001"∧C#=“002”（ SC )）
下方⑥的另一种写法也是一个很经典的错误示范！同理SC与SC1（由SC更名得到）自然连接得到，在自然连接中会合并重复项，所以新生成的表中c#栏依然要么只有001，要么只有002，右侧语句选出来一定是个空集。
Πstudent_id（σSC.C#="001"∧SC.C1#=“002”（ SC ⋈ ρSC1( SC）)）
分隔
举例⑦：查询不学习课程号为002的学生姓名和年龄（学生姓名，年龄在Student表中，课程号在SC中）
Πstudent_name，student_age（S）— Πstudent_name，student_age（σC#=“002”( Srudent ⋈ SC）)
注意⑦下方这种合并写法是错误的！因为不满足差运算的并相容性，Student、Student ⋈ SC的关系结果显然属性数目不一致
Πstudent_name，student_age（Student —（σC#=“002”( Srudent ⋈ SC）)）

所以书写关系代数的基本思路就是：

1. 检索是否涉及多个表，若不涉及，直接采用并、差、交、选择与投影

2. 若涉及多个表
   1）能否使用自然连接将多个表连接起来
   2）若不能，能否使用等值连接或θ连接
   3）还不能，那就是用笛卡尔积

3. 连接操作完成后，可以继续使用选择、投影等运算。

6.1.4 扩展的关系代数运算

6.1.4.1 广义投影

允许在投影列表中使用算数运算和字符串函数等来对投影进行扩展。

6.1.4.2 聚集函数$\mathcal{G}$

$\mathcal{G}$ 是字母G的书法体，它的下标表示采用的聚集运算。
聚集函数输入值的一个汇集，将单一值作为结果返回，例如：
以汇集{1，1，3，4，4，11}为输入：

• 聚集函数sum（$\mathcal{G}$_sum(number)(列表)），返回汇集的总和，则返回值为24.
• 聚集函数avg，返回值的平均，返回值为4
• 聚集函数min，返回汇集中的最小值1
• 聚集函数max，返回汇集中的最大值11
• 聚集函数count，返回符合条件查询的行的个数

有时在计算聚集函数前我们必须去除重复值，如果我们想去除重复，我们仍然使用前面的函数名，但将“distinct”附加在函数名后（如：count-distinct）

6.2 元组关系演算

以元组为对象和操作单位，以数理逻辑中的谓词演算为基础，按照谓词变量的不同，可以分为关系元组演算和关系域演算，其中：

• 关系元组演算以元组变量作为谓词变量的基本对象
• 关系域演算是以域变量作为此变量的基本对象

6.2.1 关系元组演算的基本形式

{ t | P(t) }
上式表示：所有使谓词P为真的元组t的集合

• t是元组变量
• t∈r 表示元组t在关系r中
• t[A]表示元组t的分量，即t在属性A上的值
• P是与谓词逻辑相似的公式，P(t)表示以元组t为变量的公式

构造P(t)还有两个运算符：∃(存在)、∀(任意)
如果F是一个公式，则∃(t ∈ r)(F(t))也是公式；如果F是一个公式，则∀(t ∈ r)(F(t))也是公式。
对于∃(t ∈ r)(F(t))，只要能找到一个F(t)为真，∃(t ∈ r)(F(t))值就为真；对于∀(t ∈ r)(F(t))，必须所有的F(t)为真，∀(t ∈ r)(F(t))才为真。

6.2.2 查询示例

举例	空白栏
检索出年龄小于20岁并且是男同学的所有学生
{ t | t∈Student ∧ t[student_sex]="男" }
检索出年龄小于20岁或者03系的所有男学生
{ t | t∈Student ∧ （ t[student_age]<20 ∨ t[D#]="03"） ∧ t[student_sex]="男" }
检索出不是03系的所有学生
{ t | t∈Student ∧ ┐（t[D#]="03"）}
检索不是（小于20岁的男同学）
{ t | t∈Student ∧ ┐（ t[student_age]<20 ∧ t[student_sex]="男"）}
检索出年龄不是最小的所有同学
{t | t∈Student ∧ ∃（ u ∈ Student)(t[student_age] > u[student_age] ）}
检索出课程都及格的所有同学（同学姓名存储在Student表中，课程分数情况存储在SC表中）
{t | t∈Student ∧ ∀（ u ∈ SC ∧ u[student_id]=t[student_id])( u[score] >= 60 ）}
检索计算机系的所有同学（学院系别存储在表Dept中）
{t | t∈Student ∧∃（ u ∈Dept ∧ u[D#]=t[D#])( u[D_name] ="计算机系"）}
检索出比张三年龄小的所有同学
{t | t∈Student ∧ ∃（ w ∈Student） ∧ （w[student_name]="张三"∧w[student_age]>t[student_age]）}
检索学过所有课程的同学(Course与SC的公共属性是课程号，SC与Student的公共属性是学生学号，所以应该进行连接)
{t | t∈Student ∧ ∃（ u ∈Course)(∃(s∈SC))（s[s#]=t[s#] ∧ u[C#]=s[C#])}

6.2.4 元组演算公式与关系代数对比应用的例子

已知：

• 学生关系：Student（S#，Sname，Sage，Ssex，Sclass）
• 课程关系：Course（C#，Cname，Chours，Credit，Tname）
• 选课关系：SC（S#，C#，Score）

①求学过李明老师讲授所有课程的学生姓名

关系代数：
使用除运算，首先找出李明老师讲授的所有课程号，用所有学生的课程去除这个课程，即可得到结果：
Π_Sname（ Π_Sname，C#（Srudent ⋈ SC ⋈ Course）÷ Π_C#（σ_{Tname=”李明“}（ Course））)

元组表达：
{t[Sname] | t∈Student ∧ ∀（ u ∈Course ∧ u[Tname]=“李明”)(∃(w∈SC))（w[s#]=t[s#] ∧ w[C#]=u[C#])}

②李明老师讲授的课程一门也没有学过的学生姓名

关系代数：
Π_Sname（Student）— Π_Sname（ σ_{Tname=”李明“}（Srudent ⋈ SC ⋈ Course）)
元组表达：
{t[Sname] | t∈Student ∧ ∀（ u ∈Course ∧ u[Tname]=“李明”)( ┐∃(w∈SC)（w[s#]=t[s#] ∧ w[C#]=u[C#]))}

③至少学过一门李明老师讲授课程的学生姓名
关系代数：
Π_Sname（ σ_{Tname=”李明“}（Srudent ⋈ SC ⋈ Course）)
元组表达：
{t[Sname] | t∈Student ∧ ∃（ u ∈Course ∧ u[Tname]=“李明”)( ∃(w∈SC))（u[Tname]=“李明” ∧ w[s#]=t[s#] ∧ w[C#]=u[C#])}

④至少有一门李明老师讲授的课程没有学过的学生姓名
关系代数：
Π_Sname（Student）— Π_Sname，C#（ Π_Sname（Srudent ⋈ SC ⋈ Course）÷ Π_C#（σ_{Tname=”李明“}（ Course））)
元组表达：
{t[Sname] | t∈Student ∧ ∃（ u ∈Course ∧ u[Tname]=“李明”)( ┐∃(w∈SC)（w[s#]=t[s#] ∧ w[C#]=u[C#])）}

6.3 域关系演算

6.3.1 形式化定义

关系域演算公式的基本形式：
{<x1,x2,……,xn>| P(x1,x2,……,xn)}
其中xi代表域变量或常量，P为以xi为变量的公式。

6.3.2 查询的例子

同样已知：

• 学生关系：Student（S#，Sname，Ssex，Sage，D#，Sclass）
• 其中 a——S#，b——Sname，c——Sage，d——Ssex，e——D#，f——Sclass
• 课程关系：Course（C#，Cname，Chours，Credit，Tname）
• 其中 g——C#，h——Cname，i——Chours，j——Credit，k——Tname
• 选课关系：SC（S#，C#，Score）
• 其中 a——S#，g——C#，m——Score

例如：检索出不是03系的所有学生
{<a,b,c,d,e,f>| <a,b,c,d,e,f>∈Student ∧ e<>“03”}

例如：检索不是（小于20岁的男同学）的所有同学的姓名
{<a,b,c,d,e,f>| ∃（<a,b,c,d,e,f>∈Student ∧ ┐（d<20 ∧ c = “男” ））}

例如：检索成绩不及格的同学姓名、课程及成绩
{<b,h,m>| ∃a,c,d,e,f,g,l,j,k(<a,b,c,d,e,f>∈Student ∧ <g,h,l,j,k>∈Course ∧<a,g,m>∈SC ∧ m<60）}

6.3.3 关系元组域关系域的比较

所以在这里可以比较一下关系域演算与关系元组演算：

关系元组演算	关系域演算
元组演算的基本形式：{ t | P(t) }	域演算的基本形式：{<x1,x2,……,xn>| P(x1,x2,……,xn)}
元组演算是以元组为变量，以元组为基本处理单位，先找到元组，然后再找到元组分量，进行谓词判断	域演算是以域变量为基本处理单位，先有域变量，然后再判断由这些域变量组成的元组是否存在或是否满足谓词判断

当然，元组演算和域演算是可以等价互换的。元组关系演算和域关系演算都是非过程化语言，域演算的非过程性最好，元组演算次之。

6.3.4 关系运算的安全性

不产生无限关系和无穷验证的运算被称为安全的。

• 关系代数是一种集合运算，是安全的：集合本身是有限的，有限元素集合的有限次运算仍旧是有限的。
• 关系演算不一定是安全的
  例如：{ t | ┐（R（t）） }，{ t | R（t）∨ t[2]>3}可能表示无限关系
  R（t）是有限的，但不在R（t）中的元素就可能是无限的，后例中的t[2]>3是无限的。
  例如：（∃u)(w(u)），（∀u)(w(u)）可能导致无穷验证
  前者被称为“假验证”，即验证所有元素是否都使得w(u)为false；后者被称为“真验证”，即验证所有元素是否都使得w(u)为true。检验所有元素就可能造成无穷。
• ∪ ∩ ∈ ⊆ ⊂ ⊇ ⊃ ∨ ∧ ∞ Φ ∉ ┐∃ ∀